さっそくだが、キミに問題だ。
「鳥は、飛ぶ」という命題は、真か?偽か?
今、答えに迷っているキミは、相当かしこい。
なぜなら、この問題に正解はないからだ。
「鳥は、飛ぶ」という命題は、
「アヒルは、飛ばない」という意味では、偽であるが、
「スズメは、飛ぶ」という意味では、真だ。
このように、真とも偽とも解せないような命題は、通常は証明ができない。
しかし、「鳥は、飛ぶ」という命題は、
「スズメは、飛ぶ」
「カラスは、飛ぶ」
「ハクチョウは、飛ぶ」
「ハクチョウAは、飛ぶ」
「ハクチョウBは、飛ぶ」
「ハクチョウCは、飛ぶ」
「ケガをしていないハクチョウCは、飛ぶ」
「小さなケガをしたハクチョウCは、飛ぶ」
「大きなケガをしたハクチョウCは、飛ぶ」
:
いくらでも命題を引き出すことができる。
このように、真か偽か判断できるレベルまで演繹して、
全体の真偽を、真の割合・百分率として表現することで、
真とも偽とも解せない命題の証明ができるようになる。
目次
命題の真偽性の問題を解決し論理の体系を統合する新概念・新証明法
嘘つきのパラドックス、自己言及のパラドックスから生まれし新定理
命題の真偽性の問題を解決し論理の体系を統合する新概念・新証明法
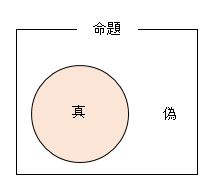
ある命題について、
演繹される命題に占める、真の割合・百分率を、

と表すことができる。
例えば…
「鳥は、飛ぶ」という命題について、
鳥の種類を基準にすると、
鳥の種類は全部でおよそ10000種、飛べない鳥はおよそ40種なので、
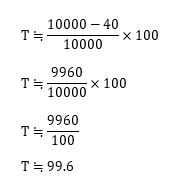
「鳥は、飛ぶ」という命題は、
鳥の種類を基準にすると、
およそ99.6%正しい(真である)、
およそ0.4%正しくない(偽である)、
ということが言える。
ある命題「P」の真理率について、
「P」=0~100
Pの否定「Pでない」は、真理率全体が100なので、
「Pでない」=100-P
命題P、Qの真理率について、
命題の命題「PならばQ」は、PとQの真偽の差(|P-Q|)の分だけ、正しくない(偽である)と言えるので、
「PならばQ」=100-|P-Q|
論理の体系は、真理値(しんりち、truth value|真偽値、しんぎち|論理値、ろんりち、logical value)を、
真(True、T)と、偽(False、F)の、2値とする「標準論理」(standard logic|古典論理、classical logic|2値論理、two-valued logic)に始まった。
ところが、命題の真偽性の問題から、真理値を、
- 真と、偽と、真偽不明のような、3値とする「3値論理」(three-valued logic)
- 真~偽と、あいまいさをもつ値とする「ファジー論理」(fuzzy logic)など
現在では、様々な領域に、細分化されている。
真理率(しんりりつ|Truth rate)は、
古代ギリシアの哲学者「アリストテレス」(前384~前322)の時代から問題とされてきた、命題の真偽性の問題を解決し、
こうして細分化されてしまった、本来一つであるべきはずの論理の体系を統合する新概念・新証明法だ。
嘘つきのパラドックス、自己言及のパラドックスから生まれし新定理
自己言及(じこげんきゅう|Self-reference)とは、自らについて言及すること。
主体が、主体(=客体)について言及すること、
主体と客体が等しくなる言及、主張、定立。
まず、自らについて言及すると、その主張に、無限のループ「再帰」(さいき)が生じる(自己言及の再帰性)。
例えば…
「この文は、日本語だ」という、この文は、
…「「「この文は、日本語だ」は、日本語だ」は、日本語だ」…
このような、再帰が生じる。
そして、自らの真偽について言及すると、次のようなパラドックス(Paradox)が生じる(自己言及の真偽性の問題)。
Q1:嘘つきのパラドックス
「私は、嘘つきだ」と発言する人について、考えてみてほしい。
…
この人が”正直”なら、「私は、嘘つきだ」という発言が嘘になり、矛盾する。
この人が”嘘つき”でも、「私は、嘘つきだ」という発言が正直になり、矛盾する。
…
これが、古代ギリシアの哲学者エウブリデスの時代(紀元前4世紀頃)から知られている、嘘つきのパラドックス(Liar Paradox)という問題だ。
A:自己言及の方程式
嘘つきのパラドックスと論理的に同じ命題、
「命題Yは、偽である」という命題Yについて、考えてみてほしい。
…
命題Yを”真”と解すると、「命題Yは、偽である」という命題が偽となり、矛盾する。
命題Yを”偽”と解しても、「命題Yは、偽である」という命題が真となり、矛盾する。
…
この命題Y(以後、Y)が矛盾しないためには、Yと「Yは、偽である」が、等しくなる必要がある。
したがって、次の方程式の答えが、このパラドックスの答えだ。
Y=「Yは、偽である」(0≦真理率≦100)
偽は、0%正しいので、
Y=「Yは、0」
命題の命題「Yは、0」は、Yと0の真偽の差(|Y-0|)の分だけ、正しくない(偽である)と言えるので、
Y=100-|Y-0|
Y=100-|Y|
Y≧0なので、
Y=100-Y
2Y=100
Y=50
つまり、この命題は、
50%正しい(真である)、
50%正しくない(偽である)、
ということになる。
そうすると、嘘つきのパラドックスの答えは、
50%正直である(真である)、
50%嘘つきである(偽である)、
ということだ。
50=…「「「50→0」→0」→0」…
無限にループしたとしても、等式が成り立つこと、矛盾しないことを確認してほしい。
次は、これを、自己言及のパラドックス(Self-reference Paradox)に応用してみることにする。
Q2:自己言及のパラドックス
自己言及命題「命題Yは、命題X」という命題Yを、数式化すると、
Y=「Yは、X」(0≦真理率≦100)
命題の命題「Yは、X」は、YとXの真偽の差(|Y-X|)の分だけ、正しくない(偽である)と言えるので、
Y=100-|Y-X|
【1】Y-X≧0、Y≧Xのとき、
Y=100-|Y-X|
Y=100-(Y-X)
Y=100-Y+X
2Y=100+X
2Y=X+100
Y=0.5X+50
【2】Y-X<0、Y<Xのとき、
Y=100-|Y-X|
Y=100-{-(Y-X)}
Y=100+(Y-X)
Y=100+Y-X
0=100-X
X=100
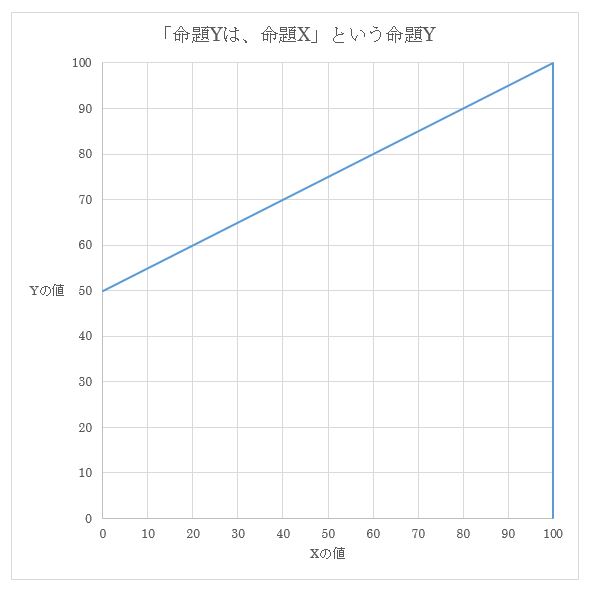
これをグラフで表すと、

不思議な一次関数のグラフになる。
A:自己言及の定理
自己言及命題「命題Yは、命題X」という命題Yについて、
真理率についての等式
Y=0.5X+50 (0≦X<100)
Y=0~100 (X=100)
が成り立つ。
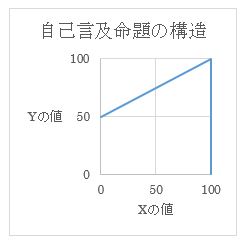
つまり、
自らその主張の正しさを主張すればするほど、その主張は正しさを増していくが、100に達すると、たちまちその主張の正しさは崩壊する、
ということだ。
この定理から、
ある理論Zが、自己言及命題Yを含むと、
【1】主張Xが、0以上100未満のとき、
Zは、Y(50以上100未満)という”正しくない部分”を含むことになり、
【2】主張Xが、100のとき、
Zは、Y(0~100)という”証明できない部分”を含むことになる。
自己言及は、【1】”正しくない部分”、あるいは、【2】”証明できない部分”を生じさせる。
自分で自分のことを主張する人に違和感を感じるのは、こういうことだ。
ps.
本記事は、”Easy ScienceBook 『ファイ』 ー科学の基本書ー”という、私の科学の集大成の記事群から抜粋したものだ。
ファイは、およそ3年間、今はなきWEBサイトにて、公開させていただいた。
その間、Prudenceさん、Vickiさん、Jennyさんをはじめ、海外の科学者の方からたくさんのコメントをいただいた。
ファイを引用してくれた方、ファイにコメントしてくれた方、ファイを最後まで読んでくれた方、本当に感謝している。